Since the early revival of neural networks, the aim of rereading in symbolical terms a function learnt by a neural network has been pursued by many researchers. Many reasons can be listed at the basis of this objective. The most obvious reason is the fact that human beings are used to discuss and communicate about scientific topics by symbols ruled by mathematical logic, with evident benefits concerning generalization, diagnosis, inquiry and explanation of the communicated matter. In other words, although no one can refuse that subsymbolic attitudes [Smolensky, 1986], such as intuition or experience, lie at the basis of practical useful actions and that they are indispensable ingredients of common sense reasoning [Sun, 1994; Sun and Bookman, 1994], we must at least be able to describe through symbols the core of these actions and their rationale, in order to extend these actions to similar operational contexts and/or to submit them to criticism, improvement and translation into formal rules. This delineates an inherent hierarchy where at low levels we locate actions and at higher levels we locate their formal explanation.

Answering the question of how the symbolic description of mental processes, in terms of rules and representations in the province of conventional artificial intelligence (AI), can be related to a subsymbolic description in terms of brain mechanisms is the so called complete reduction problem [Haugeland, 1978], as a last translation of the symbol grounding AI problem (which discusses how symbols in a symbolic system acquire meaning). Neural networks, or the connectionist paradigm in the late sense, play the role of a representative of brain mechanisms. In this context the aforementioned question translates in the more pragmatic question of designing architectures embodying both neural networks and finite states automata, where the latter represent the formal knowledge and deduction rules [Sun and Alexandre, 1997].

Various opinions regarding the links between the two (neural and automaton) modules can be found in the literature. We pass from:

1. the negation of a substantial difference between them [Verschure, 1992; 1993], reducing the neural approach to a mere technique under the usual symbolic approach;
2. a more conciliatory perspective based on the usual semeiotic distinction between concept and symbol [Dorfner et al., 1993], where a concept can be also achieved by a neural network, a symbol is a just a label, with its own algebra, to refer to a concept, and an external agent states links between them;
3. a utility point of view [Apolloni et al., 1996; Towell et al., 1990; most part of neurofuzzy literature], in which a goal oriented automatic script [Searle 1990] takes benefit from the tuning of some parameters operated by a neural network;
4. a totally subsymbolic approach [Vaario and Ohsuga, 1992], where the cognitive paradigm of an agent, aimed at surviving in an hostile environment, is completely embodied by a neural network in an evolutionary framework, in which populations of networks are decimated or increased according to fitness functions and usual genetic change (chance) rules.

Till here the high level, mostly philosophical discussion in the favourite style of the AI community. Seeing the matter from the connectionist point of view, we face a trained network and ask ourselves how to solve the complete reduction problem in this instance. In most connectionist literature on this matter, the transition from lower to higher levels is conceived as being operated by an external agent who resides on the top of an analogous hierarchy. We may think of this agent as an old parent who translates the confused stammering of his pupil into a clear sentence, i.e., who states the reference links between the naive concepts raised by the network and robust symbols. The literature concerning this more pragmatic question is reviewed in this report.

A framework for the terminology and categorization of intelligent systems as tools for modeling the brain or as machines that are characterized by an intelligent behaviour has been proposed by Bezdec [1994]. The main distinction in Bezdec's categorization is made on the basis of the abstraction level of the processing involved in each intelligent system: symbolic or subsymbolic (numerical). Historically, these two main approaches are represented by Artificial Intelligence (AI) and Neural Networks (NN), respectively. The NN approach together with other subsymbolic techniques (fuzzy logic, genetic algorithms etc) has lately been referred to as Computational Intelligence (CI) (Figure 1).

Knowledge representation in artificial intelligence systems involves the use of symbols. Among several possible definitions, we will adopt the following circular definition of symbols. A symbol is a meaningful quantity that represents a body of knowledge that may need to be accessed in processing the symbol. Stated differently, a symbol represents an abstract notion as well as relevant properties of that abstract notion. Symbolic processes transform symbol structures into other symbol structures that are relevant in a specific context. Although heuristic and linguistic knowledge used by experts can be the basis on which AI systems are constructed, the symbol grounding problem, i.e. the problem of how the symbols acquire meaning, remains one of the main problems of AI [Haugeland, 1978]. Roughly speaking, this is the top-down view of the problem of subsymbolic to symbolic mapping. Several methodologies (as fuzzy set theory, probabilistic reasoning etc.) have been used in order to support the conventional AI systems in order to bridge the gap between symbols and subsymbols. For example, fuzzy expert systems or decision trees are using numerical data in order to determine the symbolic knowledge.

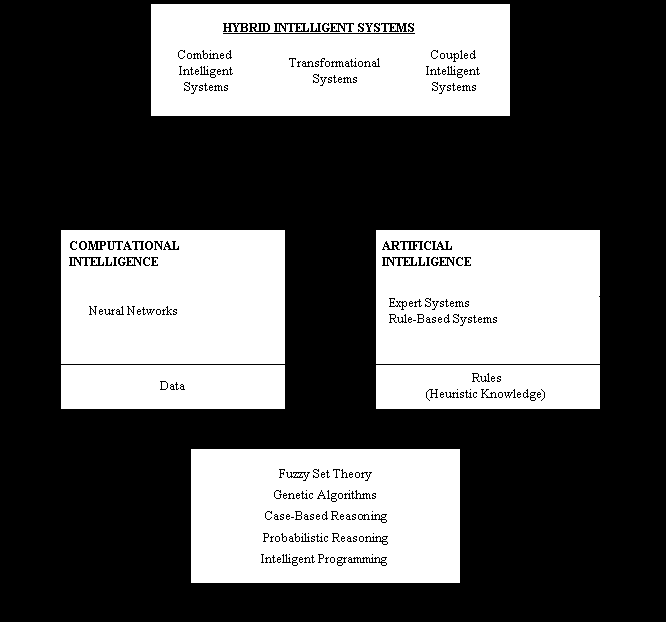
Figure 1. Intelligent systems taxonomy

On the other hand, in computational intelligent systems, knowledge is represented in a more opaque, subconceptional manner. The subsymbolic representation is usually defined by the origin of the information (e.g. sensors or database), rather than by the content of the information. Moreover, in a CI system with multiple streams of information, knowledge is usually stored in a distributed fashion. A main objective of mapping subsymbolic information into a symbolic representation is to find an abstract representation of the symbol or object, which is invariant with respect to various features (e.g. invariant with respect to position and orientation). Moreover, the representation should be such that direct links are possible to properties of the object or symbol and such that the representation can easily be used in symbolic reasoning. This problem can be viewed as the bottom-up case of the subsymbolic to symbolic mapping problem. The main approach of computational intelligence is the connectionist approach. Biologically inspired neural networks that try to model the human brain and artificial neural network models that try to emulate the intelligent behaviour of humans are the basic methods of computational intelligence. Lately, supporting methodologies like fuzzy set theory have been used in order to improve the symbolic representation and processing capabilities of NNs.

Although each of the subsymbolic and symbolic framework can specify intelligent systems by itself, the limits of each category are not clear and become increasingly vague. The emergent need for intelligent systems that can work in both the symbolic and the subsymbolic framework leads to the unification of AI and CI approaches. Fuzzy expert systems, for example, can be viewed as AI systems with subsymbolic processing extensions or as CI systems with symbolic processing extensions. Hence, the perspective that the basic method of CI is the NN approach and that the basic method of AI is the traditional symbolic processing (expert systems, rule-based systems) is mainly due to historical reasons. The main issue in the research on intelligent systems is now how the symbolic description of mental processes, in terms of rules and representations in the province of conventional AI, can be related to a subsymbolic description in terms of brain mechanisms (the top-down approach). The same question is how the subsymbolic processes of neurons, synapses and interconnections of a conventional artificial neural network can be related to the symbolic description of human logic and behaviour (the bottom-up approach). The perspective of PHYSTA is based on the bottom-up approach. One of the principal reasons that neural networks have been considered a useful vehicle for such a development is that there is an existence evidence for the solution of creating such a system (and of course answering the above questions), that of the human being.

The need for combination of AI and CI methods arises from the need for both symbolic and subsymbolic processing. This combination leads to hybrid systems. Hybridization is done not only in the sense of integrating independent AI and CI methods in order to construct an overall system, but also in the sense of the theoretical unification of AI and CI ideas (Figure 1). In the following, we will adopt a taxonomy of hybrid intelligent systems, as shown in Figure 2. This taxonomy is done on the basis of previous work by Hilario [1997] and Medsker [1995]. The basic innovation with respect to the latter lies in the use of a different terminology and in the distinction of hybrid intelligent systems into three categories. The first category, Combined Intelligent Systems, comprises systems that use NNs as tools for symbolic processing (top-down approach) and NNs that use AI concepts in order to support symbolic processing (bottom-up approach). AI and CI methodologies are combined to construct a combined intelligent system. The second category, Transformational Intelligent Systems, use CI and AI techniques to transform symbolic representations to subsymbolic and vice versa. The main operations provided by Transformational Intelligent Systems are rule insertion, rule extraction and rule refinement. The most important point is that the CI and AI methods used for this operation are stand-alone and based on conventional approaches, in the corresponding framework. The third category, Coupled Intelligent Systems, integrate AI and CI modules to produce a system with the ability to work at both symbolic and subsymbolic level. The AI and CI components are independent and communicate in a predefined way that characterize the kind of processing involved. Four types of coupling can be distinguished, namely chainprocessing, subprocessing, metaprocessing and coprocessing.

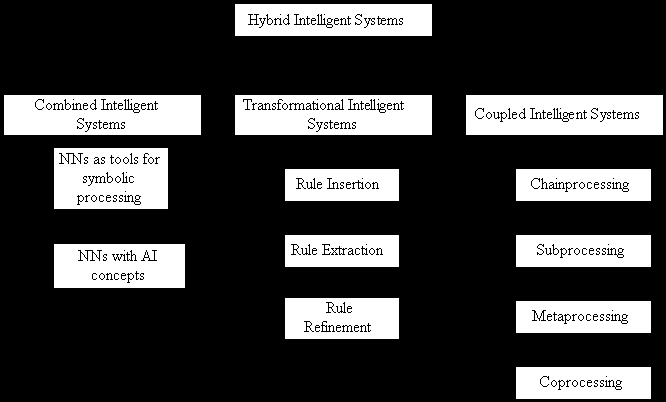Figure 2. Hybrid Intelligent Systems

In this section, some methods for solving the complete reduction problem of AI systems are reviewed. In expert systems, knowledge is represented in the form of rules that are used to carry out tasks usually performed by human experts [Dean et al., 1995]. The basis of such rules is the theory of propositional logic which uses propositional variables (true/false) and truth-functional propositional connectives, including conjunction, disjunction, negation, implication and logical equivalence. If axioms and rules of inference are provided, a sequence of inferential rules results in a proof.

Deductive retrieval systems are concerned with practical methods for logical inference. Such systems employ strategies for forward and backward chaining to expedite answering questions posed as logical formulas. Deductive retrieval systems often make use of reason maintenance systems to keep track of the justifications for adding and removing information from a database.

Reasoning in most expert systems is based on some deterministic rules. However, humans do not use deterministic rules. To illustrate this, consider a simple system with an automobile, which for simplicity is reduced to 6 elements which determine the functioning of the car: the presence of fuel (F), the indication by the gasmeter (G), the battery (B), turn over of the motor (T), the starter motor (S) and the car itself (C). The probability of the car to function p(C) can be written as

where p(G|F,B) represents the state of G given the states of F and B, etc. Humans never calculate the product of all (conditional) probabilities (which would be impossible anyway since many conditional probabilities cannot be known and since the problem would be intractable for many real-life problems, even if all conditional joint probabilities would be known). Rather, they try to estimate some probabilities for p(C|G,T), p(G) and p(T) based on daily experience, i.e. based on known probabilities. Obviously, many problems in life cannot be solved by deterministic reasoning but rather require probabilistic reasoning.

Reasoning under uncertainty may be achieved by using a probabilistic network. A probabilistic network is a directed acyclic graph G = (V,E), whose vertices V are random variables and whose edges E indicate dependencies between the random variables. Knowledge is specified by the conditional probabilities of each node given its parents. Given this knowledge and evidence Q we are interested in the posterior probability p(X|Q) of some variable X.

In tree-structured networks exact inference is possible. Consider a node X with one parent Z and n children Y_i. Define the evidence associated with the parent by Q⁺ and the evidence associated with the children by Q_i^-. If the causal support of the parent p(Z|Q⁺) and the diagnostic support of the children p(Q_i^-|X) are known, the conditional probability p(X|Q) is:

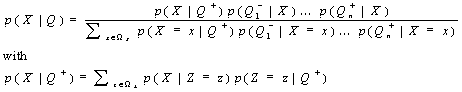
By propagating evidential and causal support through a tree-structured network, the required conditional probabilities may be acquired. In multiply connected networks precise inference is not always feasible and approximations or simulations are required (Jordan et al., 1998). The usual ways for dealing with probabilistic reasoning is to use graphical models or to use neural networks, especially neural networks which are able to learn joint and conditional probabilities.

A decision tree is represented as a directed acyclic graph comprising internal and terminal nodes. All internal nodes contain splits, which test the value of a mathematical expression of the attributes. In a univariate decision tree the test uses a single attribute, whereas multiple attributes are employed in a multivariate decision tree. As a special case of multivariate trees stand oblique trees, which use linear combinations of the attributes. Each terminal node of a decision tree has a class label associated with it. The nodes are connected by edges. The construction algorithm tries to find a rule at each node which splits the data according to some criterion giving rise to a decision tree with an exponential number of nodes at each level. The criterion is usually such that entropy or a related quantity is minimized at each node (maximum gain of information [Quinlan, 1993]). The result is a decision tree, which gives a good performance (usually with regard to classification) and which provides insight into the performance, since the rules at the decision nodes are known. These rules usually are defined in terms of if-then rules. The information-gain algorithm can be applied both for symbolic data as well as for continuous, noisy data.

Construction of a tree from a training set (tree induction) usually proceeds in a greedy top-down fashion [Murthy, 1995]:

• If all the training examples at the current node t belong to category c, create a leaf node with class c and halt.

• Otherwise,

1. score each one of the sets of possible splits using a goodness measure;
2. choose the best split s as the test at the current node, and create as many child nodes as there are distinct outcomes of s;
3. label edges between the parent and child nodes with outcomes of s, and partition the training data into the child nodes.

Several criteria can be used to define the splits at a node. The goodness of a split can be evaluated by defining an impurity function i(t) for every internal node t. Optimal splits are such that the decrease in impurity D i(s,t) due to a split s which divides the node t into a left child t_l with a proportion p_l of the data and a right child t_r with a proportion p_r of the data

is minimized. Different impurity functions may be applied. Breiman et al. [1984] use the Gini index in their CART (Classification and Regression Trees) system:

with p(i|t) the conditional probability for class i at node t. Quinlan [1993] uses the mutual information in his C4.5 algorithm to find the maximum information gain at a split in order to decide on the goodness of a split, where the information I is

In lazy learning algorithms (like the IGTree of Daelemans et al. [1997]) similarity of a new feature to stored features is used to find the nearest neighbors of the new instance. The classes associated with the nearest neighbors are then used to predict the class in the new feature. Results of Daelemans et al. [1997]) on linguistic classification tasks indicate that an accuracy similar to Quilan’s C4.5 can be achieved whereas the speed is improved considerably.

Greedy tree induction results in a tree, which is prone to overfitting of the data, and a pruning stage is necessary to obtain a decision tree which generalizes well. In the pruning stage the size of the tree is reduced by optimizing a cost-complexity measure which takes into account both the estimated misclassification rate and a complexity measure of the tree. Proper pruning requires an independent test set, cross-validation methods, or bootstrap techniques.

Techniques for developing decision trees are available for dealing with attributes with continuous values, large sets of discrete values, and in cases in which training examples are missing values for attributes. The basic decision tree methods are widely used and a large literature exists to assist the practitioner in its application (see e.g. [Quinlan, 1993]; [Breiman et al., 1984]).

Learning and adaptation are important characteristics of intelligent systems that play a central role in subsymbolic to symbolic mapping via classification. Although neural networks basically play this role, pure symbolic learning methods have been proposed as well. EITHER [Ourston and Mooney, 1994] and Labyrinth-k [Thomson et al., 1991] are two symbolic learning algorithms. The input consists of a (probably incorrect) domain theory and a set of data (and empirical knowledge). The output is a refined domain theory; in that respect both algorithms are similar to KBANN (that will be discussed later).

EITHER starts with a set of rules (domain theory) which classify a number of vectors from an input set. Some of the vectors are misclassified, due to an assumed initial set of rules which is incomplete. The set of misclassified vectors is partitioned to detect the offending rules of the domain theory. Then the ID3 algorithm [Quinlan, 1986] is fed with the correctly classified vectors and the partitioned sets of the misclassified vectors to produce the necessary corrections of the domain theory.

Labyrinth-k is an extension of Cobweb [Fisher, 1987]. Cobweb creates a knowledge structure based on some initial vectors. Labyrinth-k is applied one step before Cobweb, resulting in a structure whose formal definition is exactly the same as that produced by Cobweb. Finally, Cobweb is used, employing both structures to refine the domain knowledge. Both EITHER and Labyrinth-k refine the domain theory through direct manipulation. (As will be discussed later, the KBANN method manipulates a representation of the domain theory.)

Another interesting method, lately used to enrich AI systems with the ability of self-construction and, thus, with the ability of automatically mapping subsymbols to symbols, is genetic programming. Genetic programming (GP) is actually a method of automatic programme induction and bears a resemblance to the theory of natural selection [Koza, 1992]. The word "programme" should be considered here in the broadest possible sense, to include computer programs but also any symbolic structure. GP relies upon a mechanism which is rather counterintuitive for the layman: a population of programmes is evolved according to principles such as survival of the fittest, recombination of genomes (crossover in GP parlance) and mutation. The algorithm starts with a random population of programmes which are to be conceived as solutions (some better than others) to a problem; then each individual is assigned a value (fitness in GP parlance) which represents its quality. Programmes with low fitness are less probable to pass to the next generation and breed more children through the crossover operator. Finally, mutation is there to augment the diversity of the population. An issue of paramount importance is whether the population converges to a solution. This is an open and very prolific research area [Harik et al., 1996], [Goldberg, 1989].

According to Koza, the primary preparatory steps before applying GP to a problem are the set of terminals, the set of primitive functions, the fitness measure, the parameters for controlling the run, the method for designating a result and the criterion for terminating a run ([Koza, 1994], page 35). The set of terminals correspond to the inputs of a programme, yet undiscovered. The primitive functions can be the usual arithmetic or logical operators, mathematical functions or even domain specific functions. Each population member (programme) is made of functions and terminals. Both of these entities must be sufficient in order to produce a programme that solves (either perfectly or approximately) a problem. Functions act upon terminals or upon the result(s) returned by other functions. Thus, the programme can be evaluated in a certain environment, the result of the evaluation being the fitness measure. For instance, fitness could be the performance of a programme/chromosome on a set of data. Thus, the data are to be represented in a concise way as a programme. The parameters for controlling the run are the size of the population, the maximum number of generations and the genetic operators. The algorithm stops when the best individual (in terms of fitness) is produced or when the maximum number of generations is exceeded. The individuals (or chromosomes) that constitute the population are essentially trees. Crossover between two individuals is the exchange of subtrees.

A genetic run starts with a population of poorly performing individuals, some of which are better than others. The next generation is improved (in terms of average fitness) and, as generations pass, the population moves from heterogeneity to homogeneity; the best individuals tend to overwhelm the population. Occasionally, mutation of individuals can be introduced in order to reintroduce diversity in the population.

Genetic programming is a population based method and thus easily amenable to parallelism, similar to genetic algorithms and evolutionary programming. It lies under the umbrella of automatic programming induction and works on programmes, that is expressive symbolic structures. Furthermore, searching is performed in the space of programmes; thus, there is no need to devise a suitable representation (perhaps subsymbolic) before the run and then retract from the representation to the symbolic structure. Since GP manipulates symbols, it could be classified as being GOFAI (Good Old Fashioned AI), that is based on the physical symbol system hypothesis. The old programming technique of Divide and Conquer has been implemented in the field of GP under the name of automatically defined functions. Divide and Conquer is based on the decomposition of a problem into subproblems, which can be easily solved, and finally on the combination of the solutions of the subproblems to solve the original one. In conventional programming it is up to the user to define the decomposition, whereas in GP the subproblems are automatically defined – hence the term automatically defined functions.It is also possible and beneficial to evolve data structures in the course of programme evolution [Langdon, 1998]. Thus, it has been possible to produce structured data types (queues, lists and stacks) so as to incorporate memory in GP.

In general, AI techniques for mapping subsymbolic data into symbols by classification or decision trees are very effective when sufficient data or explicit expert knowledge is available. However, these techniques have problems with noisy data or inconsistent data. The latter typically occurs when two apparently identical data sets correspond to different classes because crucial data are missing, which would discriminate between the two data sets.

An interesting generalization of AI systems that is very effective with noisy and uncertain data is that of fuzzy knowledge-based systems. Fuzzy set theory and fuzzy logic are mathematical theories widely used in artificial intelligence [Klir and Yuan, 1995]. Fuzzy rule-based systems and fuzzy expert systems are AI systems with the ability of mapping subsymbolic to symbolic knowledge with the aid of fuzzy mathematics [Yager, 1992a]. Fuzzy partitions on the input and the output space are defined which give a linguistic meaning to numerical values. Fuzzy partitions can manage the uncertainty introduced by the inconsistency of linguistic knowledge or by noisy data. Although fuzzy knowledge-based systems provide a mapping from subsymbolic to symbolic space (supporting symbolic processing via numerical processing), they do not have learning capabilities and they can not easily adapt to numerical data (like NNs). In other words, fuzzy logic inference systems can be used to represent complex relations of subsymbolic to symbolic mapping by defining possibility distributions on the antecedents and the consequents of if-then rules, however, this representation is not powerful due to the heuristic character of the definition of these possibility distributions. The nonadaptive and heuristic behavior of fuzzy logic systems can be improved with the aid of NNs. This approach is reviewed in Section 5.1 (Combined intelligent systems).

Artificial neural networks are universal approximators and operate in a subsymbolic framework. They have been widely used for classification problems. Classification can be viewed as a first way of relating subsymbolic to symbolic information. Ideas of mapping features to symbols can be found in the basic structure of typical neural networks (such as multi-layer perceptrons, self-organizing maps etc). However, this mapping takes place to a limited extent, since traditional neural networks do not support methods for symbolic processing. With the aid of clustering and classification some general information is mined concerning the grouping of numerical data. On the other hand, methods for solving the problem of mapping features to symbols have to prove useful in terms of symbol understanding and processing. For this aim, the problem of mapping features to symbols with the aid of NNs is connected with the problem of rule extraction from already trained NNs.

Several theoretical and anatomical models have prompted a background to conscious processes. Recently "two/three stage models" have been proposed [Taylor, 1997]. Along these models, the emergence of awareness is a multistage process, from the evidentiation of semi-autonomous 'bubbles' to a neural model of the Continuum Neural Field Theory (CNFT), allowing for the rising of working memory modules out of CNFT [Alavi and Taylor, 1995; Taylor, 1997]. This model seems to satisfy issues raised by neural deficits, like neglect and blindsight, or peculiar psychophysiological effects. Furthermore several experiments have been conducted both on the neuropsychological side on the processing of auditory tasks, like word processing [Taylor, 1997; Taylor et al., 1997], and in MEG experiments devoted to explore the matching of awareness of a very object in object-non_object presentation tests [Vanni et al., 1996].

The topic of rule extraction in neural network research has raised a recent increase of interest driven by the need to develop artificial systems with near-human capabilities (although this is still remote) and analyse the manner in which humans achieve rule extraction; also by the need to understand deficits caused by brain injury as well as help build artificial systems. We will briefly describe progress being made in (a) analysing human rule following and creation, (b) investigating deficits in the above analysis and (c) creating neural networks ab initio without the use of clues from the human system. The (a) and (b) parts are being actively pursued by analysing the effects of brain damage and by means of brain imaging techniques. This relates in particular to the use of tasks which involve the creation or induction of rules, and which cannot be performed due to brain damage. Living networks involved in learning and applying rules can be observed by means of brain imaging techniques applied to normal human subjects. A review of the whole area of these various aspects of rule formation is given in [Bapi, Bugmann, Levine and Taylor, 1998].

There are several well-known tasks used to test the severity of the damage suffered by patients who have had head trauma. These involve testing working memory capabilities, in which there is holding and manipulation of representations over time in order to solve a task. Such tasks usually involve the creation of a running score, which constantly needs to be updated in order to hold material to be used at a later stage. A typical task of this sort is the n-back task, in which a subject has to press a button signifying that he has observed a letter in a sequence being successively presented and which the subject had detected n times earlier. This task is known to need the frontal lobes for n larger than one (for “holding times” longer than 10 seconds); for shorter times (for n equal to 0 or 1) only posterior cortical sites were found to be needed [Cohen et al., 1994].

There are numerous other well-known tasks for analysing the rule-following powers of humans (and animals). Thus delayed alternation choices between objects or between positions previously rewarded have been analysed extensively in monkeys, both at the psychological and the single cell level. Another very popular test of the power of rule formation is the Wisconsin card-sorting test (WCST). This uses a pack of 128 cards in which each card has a number of identical coloured shapes. The subject has to match each card he picks off the pack to a set of 4 template cards, according to the number, colour or shape of the objects on their face. The experimenter tells the subject if he is right or wrong according to the rule the experimenter has chosen (without informing the subject of it). If the subject picks correctly for ten successive cards the experimenter then changes the rule. The problem of determining the rule is thus compounded with that of being flexible enough to alter the rule the subject has just found so as to search for a new one. Moreover the results of guesses of the rule must be held in working memory over several guesses to determine their consistency with the experimenters’ response. Previously successful guesses must also be deleted from working memory when the guessed rule is found not to work any more.

There are further tests of rule formation, such as the Tower of Hanoi (in which a set of rings have to be moved from their initial stacked position on a set of pegs to a new position only following a set of movement rules) or the creation of self-ordered sequences (when different pictures have to be pointed at on a set of cards with, say, eight of the same pictures always on their face, although possibly in different positions). In the Tower of Hanoi task the rules require the subject to be able to follow them so as to plan how a set of moves would be effective; in the self-ordered tasks the rules must be created by the subject and then followed with memory being held of which responses had been earlier made.

The above tasks are used in many assessments of frontal lobe damage. Different areas of the frontal lobes have been found to be most crucial in causing deficits of various sorts in the tasks. Thus for WCST it is found that patients with damage to the dorsolateral prefrontal cortex (DLPFC) do worse than normal subjects or patients with other brain areas damaged. The DLPFC-damaged patient will tend to suffer most at persisting in using a given rule, which he has found effective, long after it has been changed by the experimenter. The processes involved can be dissected into the relation between shape and reward, in which the orbito-frontal cortex (OMPFC) has been found crucial, as compared to shifting from foreground to background, for which DLPFC is important [Dias, Robbins and Roberts, 1996].

The tasks described above, and many others, have been investigated using both PET, fMRI and MEG. The former of these does not have the beautiful temporal sensitivity of MEG (which is down to a millisecond) but they do gain in their spatial sensitivity (down to a millimetre or so as compared to the centimetre or more of MEG). However the temporal sensitivity of fMRI is now being improved considerably by using clever experimental paradigms.

The subject of brain imaging is now moving into analysis of results by structural modelling. This is an approach, which is more secure than the subtractive techniques used up to now for data analysis. There has not until now been any structural analysis of the rule-learning paradigms outlined so far. Therefore it is still too early to say what the connections are of networks of areas involved in rule induction and creation.

There have been several attempts to simulate the learning of rules and their application in the rule-learning paradigms described so far by artificial neural networks. The methods are based on recurrent networks, which can simulate working memory. These are reviewed very thoroughly in the paper of Bapi et al. [1998], to which the reader is referred.

The ACTION network proposed by Bapi et al [1998], is an attempt to devise a model which simulates the executive function (EF for short) of the frontal system. EF is defined as the “ability to maintain an appropriate problem-solving set for attainment of a future goal ” in Welsh and Pennington [1988]. The aforementioned frontal system refers to the actual prefrontal cortex of the brain, in conjunction with the areas of thalamus and basal ganglia that are closely connected with the prefrontal cortex.

Anatomical and functional data suggest that EF is distributed and hierarchical in nature. Furthermore, EF performs certain subfunctions. The authors have considered a recurrent artificial neural network that performs three of the aforementioned subfunctions, which are easily amenable to computer modeling (Figure 3). Thus, ACTION simulates a working memory, the handling of behavioral schemata and a relation between schemata and potential actions. We should bear in mind that ACTION being a neural net and performing the assumed subfunctions, constitutes a mapping from the subsymbolic to the symbolic domain.

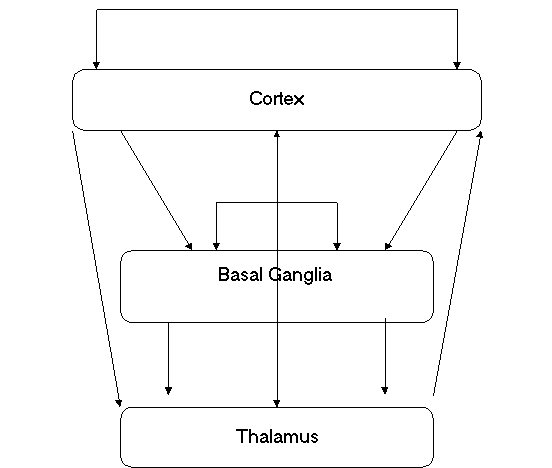
Figure 3. The ACTION network

In general, an artificial neural network maps an input vector x(t) to an output vector y(t) depending on parameters w (representing the weights of the neural network) and possibly a state vector v(t): y(t) = F(x(t),v(t),w). The state vector v(t) is only relevant for dynamic neural networks. Well-known examples of static neural networks include the multilayer perceptron (MLP): y = S(W₂ S(W₁ x)), where W₂ and W₁ are weight matrices and S represents an array of sigmoidal functions, and the radial basis function (RBF) network with Gaussian units: y = S(W G(x,m,d)), with W a weight matrix, G a mapping which contains Gaussian units with centers m and widths d.

The knowledge stored in a network depends on its architecture and on the parameter values. Usually the architecture is chosen beforehand and the parameters of the network are adapted in a learning procedure. The learning process is based on examples. It is called supervised if input data plus desired output values are specified, and is unsupervised if only the input data are given (for example with the aim to classify the inputs in clusters). Although it is known that a neural network can represent any arbitrary mapping given a sufficient number of parameters (Hornik et al., 1989), the effective mapping largely depends on the learning algorithm and on the set of training data. In particular, the training data set should sufficiently represent the underlying process and fitting to noise in the training data should be avoided.

Knowledge can be represented into the neural network in two ways: local and distributive [Lin and Lee, 1995]. Local representation is based on the one-to-one correspondence of a neuron (viewed as a building block) with a pattern represented into the network. On the other hand, in distributive representation, a pattern is represented over many processing elements and each neuron is involved in different entities. Distributive representation has a lot of advantages. First, it provides an easy way of generalization based on the similarity of the patterns represented into the network. Second, it can provide a capability of fault tolerance. If some of the processing elements break down, the network might still recognize all the patterns. Finally, the distributive representation has the advantage of using the ideas of content-addressable memory. The number of represented patterns can be increased by changing the weights of the network and not he number of neurons (up to some capacity limit which depends on the number of neurons). The main disadvantage is that it is difficult for an outside observer to identify and modify the formulation of pattern representation. This drawback decreases the ability of neural networks to map features to symbols.

Distributed representation has been used for symbolic representation via neural networks, with the aid of the coarse coding technique [Hinton, 1991]. Each neuron has a receptive field, i.e. a set that indicates the patterns involved with the specific neuron. Coarse coding uses overlapping codes to store several patterns simultaneously. Connection with fuzzy logic has been proposed, since the neuron can be viewed as a node representing a fuzzy set with its receptive field corresponding to the membership function of the fuzzy set. A way of representing recursive data structures, like trees and lists, with the aid of distributed representations, can be found in [Pollack, 1990].

Neural networks have been widely used for clustering and classification problems. While clustering mainly provides methods for grouping numerical data, classification could be viewed as a subsymbolic to symbolic mapping. Feedforward networks, like multi-layer perceptrons (MLPs) [Haykin, 1994; Bose and Liang, 1996; Schalkoff, 1997], are appropriate for various classifications tasks, although it is not clear that they can be useful for subsymbolic to symbolic mapping purposes. A more useful approach is that of tree neural networks (TNNs) [Sankar and Mammone, 1991; Guo and Gelfand, 1992]. The main idea of these networks is the combination of decision trees with feedforward neural networks using a small MLP for each decision node of the decision tree. The general structure of a TNN is shown in Figure 4. Circular nodes are decision nodes, while box nodes are terminal nodes. Each decision node has a splitting rule associated with it, which indicates whether the input pattern x goes to the right or left descendant. Decision depends on the outcome of a test involving the features f(x) and θ associated with the node, which are implemented by means of an MLP. In this case, a nonlinear function is used to combine the attributes, while a linear combination is used by oblique trees (Section 3.2). Parsing the decision nodes, the system reaches a terminal node associated with a specific pattern. TNNs can be used for difficult pattern recognition problems where the decision boundaries are complex and require nonlinear features.

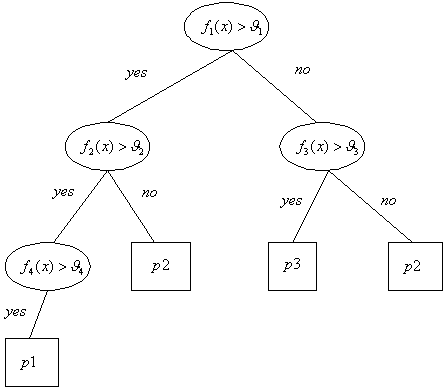
Figure 4. Classification tree of a TNN

An extension of the latter method is represented by cases where the parsing of the decision tree is hybrid [Apolloni et al., 1998]. The parser uses available syntactic rules and, in case of ambiguity, the neural network intervenes to solve the ambiguity. The same network runs on each node, thus acquiring experience descending the decision tree. The network is questioned only in case of ambiguity. At each node the network outputs a value γ for grounding the decision of adding the node to the current path from the root to a leaf (Figure 5).

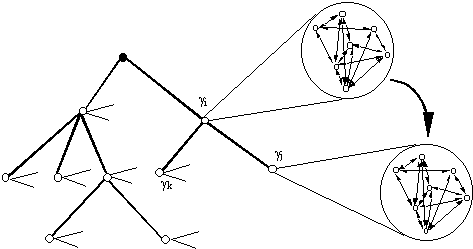
Figure 5. Descent of the neural adviser down the decision tree.

A hierarchical mixture of experts (HME) architecture [Jordan and Jacobs, 1994] is a tree-structure with gating networks on the links and expert networks on the leaves. For a two-level HME, the output of the (i,j)-th expert network m _ij is specified by the input x, a weight matrix W_ij and an array of fixed, continuous functions f: m _ij = f(W_ij x). The outputs of the gating networks depend on x and weight vectors v_ij, and sum to one for a node by using a softmax function:

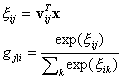
The output vector at each nonterminal of the tree is given by:

and the output at the top level of the tree is:

Jordan and Jacobs [1994] present an expectation-maximization (EM) learning algorithm for this architecture and compare the results of this approach with an MLP network and two decision tree algorithms, including CART, for the mapping of the forward dynamics of a four-link robot. Due to its tree-structure, the HME can provide insight into the manner knowledge is represented in the system.

A complete description of two stochastic processes which generate vectors x and y is provided by the joint probability distribution p(x,y). With x the input vector and y the output vector, it is the aim of supervised learning techniques for feedforward neural networks to arrive at a good model of the conditional probability distribution p(y|x) which may be employed in classification and regression tasks [Bishop, 1995; Ripley, 1996; Looney, 1997]. Unsupervised learning strategies try to give a good description of the density of the input data, i.e., a model of p(x). In contrast with these two approaches a model of the full joint probability distribution is aimed at in probabilistic neural models, like Boltzmann machines [Ackley et al., 1985; Apolloni et al., 1991].

A useful feedforward network approach is represented by the model called probabilistic neural networks (PNN) [Specht, 1990; Burrascano, 1991]. The network structures are similar to those of multilayer perceptrons; the primary difference is that the sigmoid activation function is replaced by an exponential one. Key advantages of PNNs are that training requires only a single pass and that decision surfaces approach the Bayes-optimal decision boundaries as the number of training samples grows. An interesting generalization of probabilistic networks is proposed by Kuo et al. [1993] using concepts from fuzzy set theory. The authors actually replace the statistical probabilistic function of the conventional probabilistic network with a possibility distribution function (a fuzzy measure).

A neural network may be viewed as a graphical model. Probabilistic inference can be well handled using general theory on graphical models and this moreover provides a direct link to other graphical models (e.g., classification trees, Bayesian belief networks) used in artificial intelligence. An introduction on graphical models and their relation to neural networks is provided by Jordan et al. [1998]. Whereas a tree-structured Bayesian belief network may provide direct insight to the user concerning the implementation of the probability model, densily connected Boltzmann machines do not provide such an inherent explanation. However, Boltzmann machines have incorporated a complete joint probability of inputs and outputs after training (this probability falling within a restricted family of probability distributions, at least in conventional Boltzmann machines). Based on this property, an active decision process [Kappen et al., 1995; Westerdijk and Gielen, 1998] was developed to gain insight into the implemented probability distribution. Based on partial (or completely absent) prior information, active decision aims at finding the item of input vector x, which is expected to contribute the largest information gain, about the class related to the set of input features, based on the modelled probability distribution. The basic characteristics of this procedure can be summarized as follows.

When a Boltzmann machine or mixture model with n inputs and m outputs is trained, it has stored all joint probabilities p(x₁,x₂, .. ,x_n,y₁, .. ,y_m) where x and y represent the input and output units respectively. With the joint probabilities being available, all conditional probabilities can be calculated. Now let us assume, that we have partial knowledge represented by the vector x_d. By partial knowledge, we mean, that we have knowledge about some of the n inputs. Note, that when we have no prior knowledge, x_d is the null-vector. Active decision is defined as the procedure to find that input i which provides most information given the prior knowledge x_d. Input i is defined by that i for which the expected entropy of the class distribution defined by

is minimized. Using this procedure, the neural network allows the creation of a decision tree starting with the prior knowledge x_d to obtain the desired end result, which may be a classification decision. The decisions made in the active decision process can, therefore, be depicted in a decision tree, thus providing an explanation to the user.

Basically, the difference between traditional decision trees and this procedure is, that traditional decision trees (like C4.5, CART, Lazy Learning) use an algorithm to construct a decision tree based on the data. The procedure of active decision uses a neural network to store the probability densities of the data and uses the trained neural network to develop a decision tree providing the desired result. The advantage of using a neural network is that neural networks in general have good generalization. The latter explains why the procedure of active decision gives a better performance than traditional decision generating algorithms both in classification with full knowledge as well as in classification with partial knowledge. This is especially true when data are sparse.

An anlogous active decision is performed when optimizing the lay-out of the pRAM architecture. The probabilistic random access memory (pRAM) model is a stochastic neural network, generating strings of random bits, whose joint probability distribution is modifiable through learning algorithms, in terms of conditional probabilities of any bit given the values of certain others [Apolloni et al., 1997].

Neural networks have the ability to classify and associate information, basically in a subsymbolic, numerical framework. Using fuzzy set theory and fuzzy logic principles the network becomes more flexible, more robust and can be described at a higher symbolic level. Fuzziness can be introduced either in neuron models or in the training algorithm.

Elementary types of fuzzy neurons have been investigated by Hayashi et al. [1992]. In a first type, the weights of the neuron are replaced by the membership functions of the fuzzy sets of a fuzzy partition defined on the input space. Then, the membership values are connected with a fuzzy aggregation operation in order to give a single value in the interval [0,1] as the output of the neuron. A second type comes from the modification of the basic components of the conventional neuron. The input and the weights of the neuron are fuzzy, while the operation provided by the neuron is a fuzzy set operator (multiplication of fuzzy sets etc). Another type of fuzzy neuron implements the composition of fuzzy relations which is the basis of any fuzzy relational system.

An early approach to introducing fuzziness in a conventional neural network is the fuzzy perceptron proposed by Keller and Hunt [1985]. This network has been used for fuzzy classification based on a fuzzy two class partition. In the same context, a more sophisticated method for fuzzy classification has been proposed by Pal and Mitra [Pal and Mitra, 1992; Mitra and Pal, 1995, 1997]. By incorporating concepts from fuzzy set theory into a back propagation network, an efficient scheme is obtained for the classification of data with overlapping class boundaries.

Several fuzzy neural network models utilize hyperbox fuzzy sets as the fundamental computing elements. A model of this type, developed by Simpson [1992, 1993], is the fuzzy min-max neural network. This work is based on earlier work by Carpenter et al. [1991, 1992], the fuzzy ART model. Simpson proposed two kinds of neurofuzzy systems. The first one [1992] is actually a supervised learning neural network pattern classifier, while the second one [1993] is an unsupervised learning pattern clustering system. The above networks create and refine pattern clusters and classify in a fashion similar to adaptive resonance theory. The advantage of fuzzy min-max neural networks is that they use the basic idea of fuzzy clustering, i.e. some data points can completely belong to one class but can also partially belong to another class. This characteristic is very useful in feature-to-symbol mapping. Another interesting work is that of fuzzy Kohonen clustering networks proposed by Bezdek et al. [1992], which combines the ideas of fuzzy c-means clustering and the learning strategies of Kohonen networks.

A very important generalization of neural networks stems from the need of learning symbolic knowledge expressed in fuzzy terms. This generalization includes the use of fuzzy teaching signals for the training process (reinforcement or supervised learning). An example is the work of Ishibuchi et el. [1993], who proposed a multilayer feedforward network that can learn from linguistic (symbolic) data in the form of fuzzy IF-THEN rules with the aid of fuzzy teaching signals. Lin and Lu [1995, 1996] proposed a network that can learn from both numerical and linguistic knowledge with fuzzy supervised or fuzzy reinforcement learning. This system can be viewed as a neural fuzzy expert system and is appropriate for rule extraction purposes.

In the perspective of establishing the links between low level concepts and robust symbols, several hybrid approaches have been developed. The organization of this Section follows the taxonomy introduced in Section 2 for the categorization of systems arising from neurosymbolic integration.

The category of Combined Intelligent Systems includes systems that use NNs as tools for symbolic processing and NNs that use AI concepts in order to support symbolic processing. The former systems represent a top-down design approach (start with a high-level function and proceed with the design of an appropriate connectionist infrastructure) whereas the latter represent a bottom-up approach (start from neurons and try to model high-level functions). Nevertheless, in many cases the above distinction is not obvious.

Neural expert systems attempt to weaken the disadvantages of the implicit knowledge representation in pure neural networks. They enrich neural networks with heuristics which analyse neural networks to cope with incomplete information, to explain conclusions and to generate questions for unknown inputs. This means that neural networks are endowed with other functionalities so that they have all the required features of expert systems.

The earliest attempt to build neural expert systems is due to Stephen Gallant [1988], who has developed MACIE (MAtrix Controlled Inference Engine). This system is based on a feedforward network, in which neuron outputs are spin values (± 1) produced by applying a threshold to the weighted input sum. Moreover, hidden neurons coincide with output neurons and hence, their purposes are application specific. The inputs of the system represent user’s answers to questions which may have only two values: ‘yes’ and ‘no’ encoded by 1 or –1 respectively. In addition, an unknown state is encoded by 0. The network configuration, i.e. the neural knowledge base, is created from training patterns using the so-called pocket algorithm which computes relevant weights. The algorithm works only for a single layer of neurons and that is why all states of neurons in the feedforward network should be prescribed including hidden neurons.

In the case where all inputs are known, the inference engine of MACIE computes the network function (i.e. all outputs). If some of the input facts are unknown, MACIE can still reach a conclusion and determine whether there is any chance of an output value change, should the unknown inputs become known.

Finally, MACIE provides a simple justification of inference by generating IF-THEN rules. During a consultation, the user may ask for an explanation about the particular value of an output neuron. Then the network looks for the minimal subset of the unit’s incident neurons which ensure its state, regardless of the remaining ones.

EXPSYS [Sima, 1995] is an example of Neural Expert System that has been influenced by MACIE. It differs from MACIE in two respects: a) the activation functions of the neurons are differentiable; more precisely it uses the hyperbolic tangent and b) a learning algorithm such as back-propagation can be used to train the net. The continuous activation function allows improved generalization when compared to MACIE. However, the role of the hidden units becomes more obscure. In addition to that, the inference engine as well as the explanation heuristics are more complicated. EXPSYS can also handle incomplete information by introducing the notion of interval states of neurons [Sima, 1992]. Neurons can assume any value in the [-1,+1] range. A defined piece of information is denoted by a single value within this interval, whereas ignorance is encoded by the whole range [-1,+1]. Due to the novel concept of the interval, the activation functions of the neurons as well as the learning algorithm have to be modified.

After training the EXPSYS, the user may provide input data for some of the input variables, to receive a partial conclusion along with a confidence factor. The user can also provide complete input data which will improve the confidence of the conclusions. The user can ask EXPSYS to justify a conclusion. In that case, EXPSYS will determine certain neural inputs which have greatly influenced the conclusion. These inputs will be presented to the user along with a weight measure denoting their importance.

The KBANN [Towell et al., 1990], which stands for Knowledge-Based Artificial Neural Network, integrates propositional calculus with neural learning. More precisely, a set of rules designates a domain theory which is partially correct. This set is integrated into a neural network. The neural network is trained, thus refining the rules. Finally, the rules are extracted from the network. However, rule extraction is not an official part of the KBANN algorithm.

The authors of KBANN have established a correspondence between the domain theory and a neural network which appears in the following table. This table also sketches the method of knowledge insertion into the neural network.

Domain Theory	Neural Network
final conclusion	output units
intermediate conclusions	hidden units
supporting facts	input units
antecedents of a rule	highly-weighted links

A simple way to perform the phase of rule refinement and enhancement of the domain knowledge is to use backpropagation.

The authors have compared KBANN to empirical learning systems, i.e. systems that learn only from data, and to systems which learn from theory and data, like EITHER or Labyrinth-k. It seems that KBANN generalizes better than any other empirical based method. However, it also exhibits certain limitations:

• It cannot handle rules with variables or cycles.
• There is no mechanism for handling uncertainty in the rules.
• The symbolic meaning of the initial neural network is ignored by KBANN, which results in long training times.
• Finally, there is no mechanism for dynamically changing the topology of the neural network.

An algorithm called KT [Fu, 1994], which stands for Knowledgetron, has been developed in order to extract propositional rules from a trained, feed-forward, multilayer perceptron. The input to this algorithm consists of the structural parameters of the network (number of layers, number of nodes, weights and threshold values) in addition to certain other parameters. The output is a set of rules of the following form:

if A₁⁺ , .... , A_i⁺ , .... , ù A₁^- , .... , ù A_j^- then C (or ù C)

where A_i⁺ is a positive antecedent (an attribute in the positive form), A_j^- a negated antecedent (an attribute in the negative form), C is the concept, and the symbol ‘ù ‘ stands for «not». Hence, there are two types of rules: confirming and disconfirming. A pos-att for a concept C is defined to be an attribute designating a node which directly connects to the node corresponding to C and the connection weight is positive. A neg-att for C is defined in the same way except that the connection weight is negative. In a confirming (disconfirming) rule found by KT, a pos-att exists in the positive (negative) form and a neg-att in the negative (positive) form.

An attribute of n values is represented by n attributes, so an attribute is actually an attribute-value. Generally, there is a corresponding rule for every hidden or output node of the network. It is however possible to fuse rules, should some symbol designate hidden units which do not correspond to predefined attributes. The KT algorithm can be trivially extended, such that a «belief value» is attached to every extracted rule, which allows for inexact reasoning.

The KT algorithm is based on the principle that a neuron is fired whenever the weighted sum of its inputs exceeds a certain threshold. The algorithm heuristically searches through the rule space expanded in terms of combinations of attributes, which are distinguished into pos-atts and neg-atts according to the concept for which the rules are formed. To form confirming rules, the algorithm will first explore combinations of pos-atts and then use neg-atts in conjunction to further consolidate positive combinations. Similarly, to form disconfirming rules, the algorithm will first explore combinations of neg-atts and then use negated pos-atts in conjunction. The distinction between these two kinds of attributes considerably reduces the size of the search space. Furthermore, through layer-by-layer search, the overall search space is exponential with the depth of the network.

A novel method for the classification of structures by neural networks has been proposed by Sperduti and Starita [1997]. Structure or graph manipulation can be very useful in a variety of domains such as classification in molecular biology and chemistry, heuristics discovered by neural networks for automated theorem proving, geometrical and spatial reasoning in robotics etc. The authors propose a generalization of a recurrent neuron, whereby it is facile to map graphs to a neural network. This neural network encodes a graph in its structure; its output units form a vector representing the graph, which can be fed to an ordinary classification network. The point of the authors is that their system learns a problem specific graph representation rather than relying on predefined ones.

The main concept is the generalized recursive neuron whose output is defined as:

where f is a sigmoidal function, N is the number of inputs l_i to neuron x, out(x,j) is the j^th output of neuron x, and w_j’ are the recursive connection weights. A network made of generalized neurons corresponding to a graph is constructed as follows: the number of neurons equals the number of graph nodes and the edges of the graph are transliterated into neural links. The training data are made of a series of graphs, which are incorporated so as to constitute a super graph. Usually, training involves the use of the generalized neural network as a front-end module to a supervised classification network. Adjustment of the weights of the generalized neural network is performed through an error signal provided by the classification network.

The above methodology is closely related to the RAAM (Recursive Auto-Associative Memory) architecture, proposed by Pollack [1990]. The RAAM is an odd-number (generally three) layered hierarchical network with the same number of units in the input and output layers and a smaller number of units in the hidden layer, as sketched in Figure 6. Its objective is to reproduce on its output units the activation pattern of the input units, thus acting as an auto-associative neural network. The signal, coded as the activation state of the nodes of the first (input) layer, flows through the network. The connections between the layers must induce an identical signal in the output nodes. Thus, the hidden layer constitutes a bottle-neck which collects, in the activation states of its nodes, a compressed representation of the input. The RAAM is essentially an encoder of structures. The part from the first to the second layer is the encoder since it provides a compressed representation, whereas the part from the second layer to the third is the decoder.

Figure 6. A RAAM device

An extension of RAAM is the LRAAM model [Sperduti et al., 1995; Sperduti and Starita, 1997], which can be used in conjunction with a classifier network to classify labeled structures. The LRAAM model (Labeling Recursive Auto-Associative Memory) is an encoder of labeled structures/graphs. It is made of layers of records, where the first layer encodes the labels (N_L units) and the links (n*N_h units) of the corresponding nodes – n in number- of the graph. The second layer is made of N_h units (the hidden units) and finally the third layer is exactly the same as the first layer (in structure only, not in the weights of the connections). The connection weights are determined during training. The training signal is produced by a classification network which is attached to the LRAAM network.

A recurrent neural network can be programmed to behave like a given deterministic finite state automaton (DFAs). An interesting method has been developed [Omlin and Lee Giles, 1996b] which is provably stable, in the sense that the neural network correctly classifies strings of arbitrary length. The structure is based on second order recurrent neural networks. The number of external inputs equals the number of symbols of the automaton's alphabet, each input corresponding to a specific symbol of the alphabet. The hidden units are the states, and the connection weights are directly related to the transitions of the automaton. Omlin and Lee Giles have proved that under certain conditions their network is stable, i.e. it behaves exactly like the automaton for arbitrary long strings

Fuzzy systems are numerical model-free estimators. While neural networks encode sampled information in a parallel-distributed framework, fuzzy systems encode structured, empirical (heuristic) or linguistic knowledge in a similar numerical framework. Although they can describe the operation of the system in natural language with the aid of human-like if-then rules, they do not provide the highly desired characteristics of learning and adaptation.

The use of NNs in order to realize the key concepts of a fuzzy logic system enriches the system with the ability of learning and improves the subsymbolic to symbolic mapping. Neural network realization of basic operations of fuzzy logic, such as fuzzy complement, fuzzy intersection and fuzzy union, has been proposed ([Pao, 1989; Hsu et al., 1992]). The activation function of neurons is then set to be one of the three basic operations mentioned above in order to provide fuzzy logic inference. Another approach is to use the ordered weighted averaging neuron [Yager, 1992b] for representing fuzzy aggregating operations. A feedforward network can also be used to represent the membership function of a fuzzy set.

A connectionist approach of fuzzy inference has been proposed by Keller et al. [1992b]. The network is referred to as fuzzy inference network and implements a rule of the form

IF X₁ IS A₁ AND X₂ IS A₂ AND … AND X_n IS A_n THEN Y IS B

For choosing the parameters of the fuzzy inference that are associated with the parameters of the network, a training algorithm has been proposed.

Another approach is the generalization of the Takagi-Sugeno-Kang inference model [Sugeno and Kang, 1988]. Neural-network driven fuzzy reasoning, proposed by Takagi and Hayashi [1991], constructs the antecedent part of a fuzzy system using a back-propagation network. A lot of interesting ideas, useful in symbolic to subsymbolic mapping, can be found in this approach and especially in the steps of selection of input-output variables and clustering of the training data.

The issue of identifying the fuzzy rules and tuning the membership functions of fuzzy sets using neural networks and training algorithms has been widely studied. Horikawa et al. [1992] proposed fuzzy modeling networks in order to realize the fuzzy reasoning process through association of its parameters with the weights of a backpropagation learning neural network. According to this method, the basic parameters of the fuzzy model can be automatically identified by modifying the connection weights of the network. Another approach to this problem related to fuzzy control has been proposed by Lin and Lee [1995] (chapter 19), who introduced the fuzzy adaptive learning control network (FALCON) to study hybrid structure-parameter learning strategies. Structure learning algorithms are used to find appropriate fuzzy rules and parameter learning algorithms are used to fine tune the membership functions and other parameters of the fuzzy inference system. Actually, Lin and Lee proposed a number of different architectures and learning procedures. The first model, the FALCON-H, is a multi-layer feedforward network which represents, in a connectionist structure, the basic elements and functions of a fuzzy logic controller. It is supported by a hybrid learning algorithm that consists of two separate stages, combining unsupervised learning and supervised gradient-descent learning (backpropagation). Structure learning, which can lead to the extraction of rules, is based on the adaptive fuzzy partitioning of the input and output spaces and the combination (association) of these partitions. In order to provide a more flexible fuzzy partitioning, Lin and Lee proposed the FALCON-ART model, applying adaptive resonance theory (ART) learning. The above models require precise training data to indicate the desired output through a supervised learning process. Unfortunately, such type of data may be very difficult or even impossible to obtain (especially for the feature-to-symbol-mapping). The FALCON-R model, developed to remedy the above problem, is a reinforcement learning neurofuzzy system that performs automatic construction based on a right-wrong (reward-penalty) binary signal. The applied learning algorithm of FALCON-R is complicated, since it is designed to use deterministic reinforcement feedback, stochastic reinforcement feedback and reinforcement feedback with long time delay. Berenji and Khedkar [1992] have proposed another neurofuzzy control system using reinforcement learning, the generalized approximate reasoning-based intelligent controller (GARIC). All the above models have been well tested for fuzzy control applications. Their advantage is that they have the ability to support automatically the extraction of fuzzy inference rules. Multi-layer perceptrons have also been used for the more complex case of multistage fuzzy inference [Uehara and Fujise, 1993]. The method is based on the propagation of linguistic truth values and constitutes an interesting example of complex symbolic processins arising from a subsymbolic (numerical) framework.

An interesting connection of fuzzy systems and neural networks has been proposed by Pedrycz [1991], who pointed out the conceptual role of fuzzy relation equations in the description and evaluation of fuzzy inference systems. For the rule extraction problem, input-output data are available and the rules that linguistically describe the system have to be found. In this case, a fuzzy relation that represents the system can be determined from the data with the aid of a fuzzy relational equation involving three fuzzy relations:the first and the second concern the symbolic representation (fuzzy partitions) of the input and the output space respectively, while the third represents the correspondence of these fuzzy partitions. Neural networks have been proposed by Pedrycz [Pedrycz, 1991; Pedrycz and Rocha, 1993; Hirota and Pedrycz, 1996] to solve the above fuzzy relation equation, making use of generalized logical types of neurons. The rules of the fuzzy system can be extracted from the solution of the so-called inverse problem of fuzzy relational equations (the finding of input fuzzy sets that correspond to the output fuzzy sets). Another approach for solving fuzzy relation equations with the aid of neural networks has been proposed by Wang [1993].

Several methods are described next which aim at extracting, inserting or refining propositional rules in trained neural networks. Some of these methods are decompositional, in the sense that the focus is on extracting rules at the level of individual (hidden and output) units [Andrews et al., 1995]. The inputs (outputs) of a unit are interpreted as the antecedents (consequents) of a rule. Stretched values (to -1, 0 or 1) of the weights of the incoming synapses determine the antecedent condition and a heaviside, or its fuzzified sigmoidal, activation function determines the consequent. The rule is true whenever its antecedents are true, which in the domain of neural logic is interpreted as the situation in which the weighted inputs of a unit surpass the threshold of that unit regardless of the specific values of inputs. In terms of propositional logic, the most complex form emerging from this analysis is the N-of-M form, i.e. at least N out of the M input units need to be active in order to overcome with their unitary contribution a threshold value. (This interpretation was adopted for the first time by Gallant in MACIE [Gallant, 1988].) A more sensitive use of the synaptic weights allows to figure the above input boolean variables as indicator functions of (crisp or fuzzy) sets of values of other non boolean variables.

Other rule extraction methods are usually classified as pedagogical, in the sense that the network is treated like a black box, whereby rules are extracted. Hence, the activation functions of individual neurons or the structure of the network are completely irrelevant. The whole neural network is used as a sensitivity tool to state preconditions directly on the joint range of input vector's components with respect to the consequent appearing on the output vector.

RULEX [Andrews and Geva, 1994; 1995] is a technique of rule extraction from a trained CEBP (Constrained Error Back-Propagation Network). The derived rules belong to the class of propositional logic and have the if-then form. The algorithm for rule production is quite efficient since it is based on a direct interpretation of the parameters of the CEBP network. Furthermore, it is possible to refine a set of rules by inserting them into the CEBP network, training the network and then extracting them.

A CEBP network is a multi layer perceptron, where the hidden layer is comprised of a set of sigmoid based local response units (LRUs) that perform function approximation and classification in a manner similar to radial basis function (RBF) networks. More precisely, each LRU can be considered as a representation of a class or as a local bump, made of a superposition of ridges, each ridge corresponding to a dimension of the input vector. Thus, for the LRU to be active, all of its ridges must be active and the extracted rules must have the following form:

IF Ridge₁ is Active

AND Ridge₂ is Active

AND Ridge_n is Active

THEN

Input is in the TARGET category.

The active range for each ridge can be calculated from its centre, breadth, and steepness (c_i, b_i, k_i) weights in each dimension. This means that it is possible to directly decompile the LRU parameters into a conjunctive propositional rule of the following form:

IF c₁ - b₁ + 2k₁^-1 £ x₁ £ c₁+ b₁ - 2k₁^-1

AND c₂ - b₂ + 2k₂^-1 £ x_{2 £} c₂ + b₂ - 2k₂^-1

....................

THEN

the pattern belongs to the «Target class»

For discrete valued input it is possible to enumerate the active range of each ridge as an OR’ed list of values that will activate the ridge. In this case it is possible to state the rule associated with the LRU in the following form:

IF V_1a OR V_1b ... OR V_1n

AND V_2a OR V_2b ... OR V_2n

..................

AND V_Na OR V_Nb ... OR V_Nn

THEN

the pattern belongs to the «Target Class»

The technique provides a mechanism for refining the extracted rules so as to render the rules comprehensible. Rule readability can be enhanced by removing redundant antecedent clauses (i.e., input dimensions that are not used in classification) from the extracted rule or by removing redundant rules (i.e., replacing two rules by a single more general one). It is also possible to remove antecedent clauses that could be better expressed as the negation of the directly extracted antecedant condition.

It is also quite straightforward to incorporate propositional rules in the CEBP network; in this case a rule is transcribed as an LRU whose parameters stem from the form of the rule. More specifically, the active range of a ridge is determined by the x_lower and x_upper parameters, which in turn are defined so as to cut off the range of antecedent clause values. Having determined the active range of the ridge, the ridge centre and steepness parameters are calculated.

Finally, the CEBP network is suited to rule refining of partially correct, incomplete or inaccurate knowledge. As mentioned, rules are encoded as LRUs which grow, shrink and move during training to form a more accurate representation of the knowledge embedded in the training data.

Discrete-time recurrent neural networks can be trained to correctly classify strings of a regular language. Rules defining the learned grammar can be extracted from networks in the form of deterministic finite-state automata (DFAs) by applying clustering algorithms in the output space of the recurrent state neurons.

A second-order recurrent network is trained with certain positive and negative examples from the language of the automaton. This network comprises N recurrent hidden neurons labeled S_i. Each recurrent neuron, which has a sigmoid activation function, is connected to all other recurrent neurons and accepts as input the weighted sum of their outputs at the previous time instant. Additionally, each neuron is connected to a set of external inputs I_k (1£ k£ L). The activation of neuron S_i takes the form

where the real-valued weight w_ijk refers to the connection from unit j to unit i with respect to the k-th external input. The training method is based on the RTRL (Real Time Recurrent Learning) net of Williams and Zipser which computes the partial derivative of a quadratic error function with respect to all weights W_ijk.

The algorithm [Omlin and Lee Giles, 1996a], employed to extract a finite state automaton from a network, is based on the observation that the outputs of the recurrent state neurons of a trained network tend to cluster. The authors have theorized that those clusters correspond to the states of the finite-state automaton learned by the network.

The extraction algorithm divides the output of each of the N state neurons into q intervals of equal size, yielding q^N partitions in the space of outputs of the state neurons. Starting in some defined initial network state, the trained weights of the network will cause the current network state to follow a continuous state trajectory as symbols are presented to the input. The trajectories are the transitions of the automaton. The algorithm, starts from a certain partition and traverses the space of the partitions, by creating a novel automaton state for each newly visited partition. The algorithm terminates when no new states can be created.

It should be noted that the rule extraction algorithm is not restricted to second-order neural networks and can be applied to any discrete-time neural network. Furthermore, not all of the q^N partitions are visited, which in any case would be unfeasible. The number of partitions visited is related to the number of input strings used during the rule extraction process.

The parameter q, which defines the number of partitions, has a profound influence on the number of states of the automaton. Experiments have established that small values of the q parameter lead to automata with a fewer number of states.

Thrun's method [Thrun, 1995] extracts "if-then" rules from feedforward networks, but it can be extended to recurrent networks as well. The method is called Validity Interval Analysis (VI-analysis for short) and is based on the discovery of activation intervals for the activations of a subset of the network units. Naturally, the intervals are subsets of the [0,1] range of values assumed, in theory, by the sigmoidal function. There are several ways to generate the intervals; next we shall describe the specific-to-general method. But first, let us assume (for simplicity’s sake) that there is only one output unit designating two concepts (C and ù C). The method starts with a degenerate interval Χ which contains one training instance belonging to output class C. Therefore, the rule is Xà C, which is transliterated as: all training instances in hypercube X are in class C. Then X is subject to gradual enlargements, checking with VI-analysis whether the enlarged X is still a member of C. This checking is performed using linear programming.

The author addresses certain issues that arise when following his method. The first is the question of speed, which depends on the algorithm employed for linear programming. Another issue is the use of a rule language that is richer than the currently employed "if then" structure. Finally, there is also the issue of linear optimization per se. It would be possible to employ non-linear optimization methods extending over several layers of weights. In this case the set of rules would be more concise, but the question is whether it would be less accurate.

Setiono and Liu [1995] proposed a way to extract propositional rules of the form if then else from a feed-forward neural network. Their method is based on a three step approach:

1. Weight decay is performed while the net is trained.
2. The activation values of hidden units are discetized.
3. Rules are extracted by examining the discretized activation values of the hidden units.

The rationale of the first step is to limit the number of links and the number of hidden units. That is because links represent preconditions and hidden units designate concepts. Hence, network pruning which is a result of weight decay (a hidden unit is erased if it leads to or stems from a weak link) produces comprehensible rules. The discretization of the activation values of the hidden units is performed through clustering. A likely effect of clustering is the deterioration of the performance of the net. In that case the clustering criterion can be relaxed, thus more clusters will be produced which will better reflect the activation values of a neuron. The rules can be extracted by examining the possible combinations in the network outputs.

Narazaki et al. [1996], deal with the problem of rule extraction from neural networks in a novel way: they base their method on the function approximated by the network, rather than considering connection weights. The latter approach is followed by other methods, such as Fu's Knowledgetron, which interpret the weights as correlation information, i.e. correlation between an input and an output instance. The method includes a feedforward neural network, whose operation can be conceived as approximation of a membership function, at least in classification problems.

Narazaki's approach is based on the discovery of monotonic regions of the input space. A monotonic region includes a set of input patterns that belong to the same class and have the same sensitivity pattern. Each monotonic region has a centre. A sensitivity pattern for a monotonic region assumes the values {+1,-1,0}and determines what happens as we move away from its centre. For the sake of simplicity let us assume that the input domain is one-dimensional and there are two categories for the input data. The monotonic regions are also one-dimensional. Thus, the sensitivity pattern +1 for a specific monotonic class will denote that as an input variable increases, so does the membership degree. The formal definition of the sensitivity measure is given as the sign of a derivative. Another reason for incorporating sensitivity information is that it provides better generalization ability.

The extracted rules have the form:

where (x₁,x₂,…,x_n) is an input vector and g₁ⁱ , g₂ⁱ , … , g_nⁱ are the coordinates of the centre of the monotonic region M_i. The expression “around” is associated with a closed interval in the domain of x_i. The computational complexity of the algorithm is O(M²) where M is the cardinality of the instances in the input domain.

A method called TREPAN (extraction of tree-structured representations from trained networks), whereby propositional rules are extracted from a neural network with the aid of a decision tree, has been proposed in [Craven and Shavlik, 1996]. A neural network is trained on a data set. Then a decision tree extraction method is applied on the data set using the neural net as an oracle. The result is a set of rules which is nearly as accurate as the original network. Furthermore, the rules are more accurate and more comprehensible than in the case that pure decision-tree methods were employed. The authors tested their method on a noisy time series task, the prediction of the Dollar- German Mark exchange rate. TREPAN assumes nothing about the architecture or the training method of the neural network. Actually, the neural network is dealt with as a black box. In the task considered here, the neural network was trained with a technique known as clearning [Weigend et al., 1996].

The second step of the TREPAN algorithm is the extraction of a decision tree, which is different from conventional decision tree algorithms in certain respects:

• Membership queries and the Oracle. The classification of an instance is performed by asking the neural network – hence the term Oracle. The instances which are classified are generally more than the training examples of the network. Actually, the term instance denotes a member of the domain for the neural network, whereas a training set is a subset of the domain.
• Tree expansion. Whereas in most decision tree algorithms trees grow in a depth-first manner, TREPAN employs the best-first principle. Best is the node which when expanded will increase the classification accuracy of the tree. There exists a validation set which specifies the best node.
• Stopping criteria. The tree growth stops when any of two global or one local criterion occurs. The first global criterion is the size of the tree, which determines its comprehensibility. The second global criterion is related to the growth of the tree which is done in best-first manner. The local criterion indicates that node expansion stops, when all training examples fall in the same class.

Coupled Intelligent Systems incorporate complete symbolic and connectionist components [Hilario, 1997]. They achieve effective functional interaction between conventional neural networks and symbolic processors like rule interpreters, parsers, case-based reasoners and theorem provers. Coupled Intelligent Systems can be distinguished along different aspects, such as the target problem or task domain, the symbolic (e.g., rule-based reasoning, case-based reasoning) and neural (e.g., multilayer perceptrons, Kohonen networks) models used, or the role played by the neural (N) and symbolic (S) components in relation to each other and to the overall system. Taxonomy of hybrid systems based on the degree and the mode of integration of the N and S components is given in the sequel.

The degree of integration is a quantitative criterion and one may distinguish between loose and tight coupling. In loosely coupled systems, interaction between the two components is clearly localized in space and time: control and data can be transferred directly between components, or via some intermediate structure or agent. In tightly coupled systems, knowledge and data are shared between components via common internal structures. Shared structures may be as simple as mere links and pointers between components (Giacometti 1992) or they may be more complex in nature, like nodes shared between the symbolic and the connectionist network (Hendler 1989).

Four integration schemes are distinguished according to the way in which the neural and symbolic components are configured in relation to each other and to the overall system, namely chainprocessing, subprocessing, metaprocessing and coprocessing (Figure 7).

In chainprocessing mode, either of the N or S modules may be the main processor whereas the other takes charge of pre and/or postprocessing tasks. [Ciesielski et al., 1992] and [Hayes et al., 1992] outline a system in which a symbolic module is assisted by a neural preprocessor. A feedforward neural network trained by backpropagation is used to provide the qualitative states to be used as the input to an expert rule-based system in a respiratory monitoring application. The combination of ITRULE and neural networks as presented in [Goodman, 1989] and [Greenspan et al., 1992] is an example in which a rule induction algorithm like ITRULE is used for preprocessing. Training is carried out for the preprocessing module and rules are then compiled into the neural net which is used for inferential and not for generalization purposes. Symbolic preprocessing of conventional neural networks alleviates such problems as learning time, noise and redundant features. Piramuthu and Shaw [1994] perform symbolic preprocessing by using decision trees as feature selectors reducing training time. Problem solving time can be reduced as well in a similar fashion (WATTS-Wastewater Treatment System, [Krovvidy and Wee, 1992]).

Figure 7. Taxonomy of Coupled Intelligent Systems

In subprocessing mode, one of the two components is embedded in and subordinated to the other, which acts as the main problem solver. Typically, the S component is the main processor and the N component the subprocessor. The symbolic main processor may delegate to neural networks certain phases or subtasks of the application task that it does less well than NN (INNATE/QUALMS [Becraft et al., 1991] and LAM^TM [Medsker, 1994]). Alternatively, it may call on NN to perform specific internal functions independently of the application task at hand like rule interpretation [Giambasi et al., 1989] and initialization of a theorem prover (SETHEO, [Suttner and Ertel, 1990]).

In metaprocessing mode, one module is the base-level problem solver and the other monitors, controls or performs model refinement of the first module. Both symbolic and connectionist modules can assume a metalevel role in hybrid systems. Carnegie-Mellon’s ALVINN is an example of symbolic metaprocessing for guiding autonomous vehicles [Pomerleau et al., 1991]. Robotic Skill Acquisition (RSA) is also an example of a symbolic metaprocessor which supervises both symbolic and baselevel components for developing robots able to perform complex tasks [Handelman et al., 1992]. On the other hand, Kwasny and Faisal’s [1992] natural language parser and Gutknecht and Pfeifer’s [1990] problem solver are examples of neural metaprocessing.

In coprocessing both N and S modules are equal partners in the problem solving process: each can interact directly with the environment, each can transmit information to and receive information from the other. Both can compete under the supervision of a metaprocessor. In SYNTHESIS [Giacometti, 1992], the same diagnostic task is executed by a rule-based system and a prototype-based neural network that learns incrementally. An alternative example of cooperative coprocessing by distribution of specialized subtasks is a system where a neural network and a decision tree work together to detect arrythmia in heart patients [Jabri et al., 1992].

The above described rich taxonomy and characterization of algorithms and representations is the basis for the development of a theory and methodology in the PHYSTA Project. Moreover, PHYSTA will investigate a different perspective. According to this, the rule extractor is not an external agent but a rule located in the mentioned hierarchy, i.e. a piece of neural network by itself. Thus, rather than an external subroutine, we are looking for an inner loop priming symbols from synapses. Let us schematize the problem in this way: all that exists is a plenty of neurons interconnected through plastic synapses. Plasticity means that synapses are capable of answering to external stimuli by modifying their weights according to some entropic rule. Plasticity plays the double role of modifying the synaptic weights and, as an extreme consequence, modifying the neural network architecture. Thus, as a solution of the mind-brain dilemma [Verschure, 1997], in place of searching for an architecture and weights that may be optimal for a special brain task, we try to solve the same search problem under the target of optimizing the implementation of the above entropic rules. Stated in other words, we look at physiological models in order to develop realistic models for passing from features to symbols. Starting from already trained neural networks, we can skip the wide chapter of efficient and realistic learning algorithms. Rather, we focus on neural network architecture and dynamics.

A direct approach for passing from synapses to symbols tries to "open" the trained network in order to recognize symbolic structures. We acknowledge that this is an efficient way only in elementary cases, where the information content of the connection weights is very low. Actually, these cases must occur when the brain tries to organize in a very compact and unambiguous form the detailed knowledge experienced at subsymbolic level. We can expect that in this case the network wires simple circuits, such as boolean aggregates, by itself, still as a result of optimization of some entropic rules; our way of discovering these circuits must be different for sake of computational efficiency. We can discover boolean formulas, for instance, by analysing connections between hidden and output nodes, but this will be successful under the condition that the network has been trained for a very long time on a very large training set according to an appropriately devised error function and a suitable learning procedure.

Otherwise, we can shorten this subsymbolic process by symbolically training the high-level network through a process that is not neurophysiological-like, but agrees with the neurophysiological learning process hypothesized to occur in the brain. One of the most relevant facilities that distinguishes optimization from learning and is available under this second strategy is the capability of generating suitable examples by ourselves (in a sort of unconstrained active learning [Cohn et al., 94]) instead of hopefully waiting for them from the environment. The output of this process can be exactly the formal knowledge we are searching for.

1. Ackley D.H., Hinton G.E. and Sejnowski T.J. (1985), A learning algorithm for Boltzmann machines. Cognitive Science 9:147-169.
2. Alavi F. and Taylor J.G. (1995), A global competitive neural network. Biol. Cybernetics, vol.72, 233-248, 1995.
3. Andrews R. and Geva S. (1994), Rule extraction from a constrained error back propagation MLP. Proc. 5th Australian Conference on Neural Networks, Brisbane, Queensland, pp. 9-12.
4. Andrews R. and Geva S. (1995), Inserting and extracting knowledge from constrained error back propagation networks. Proc. 6th Australian Conference on Neural Networks, Sydney.
5. Andrews R., Diederich J. and Tickle A.B. (1995), Survey and critique of techniques for extracting rules from trained artificial neural networks. Knowledge-based Systems, 8 (6), 373-389.
6. Apolloni B, Bertoni A., Campadelli P. and de Falco D. (1991), Asymmetric Boltzmann Machines. Biological Cybernetics, 66, 61-70.
7. Apolloni B., Piccolboni A. and Sozio E. (1996), Hybrid symbolic subsymbolic system for controlling a single link flexible arm. J. of System Engineering, 6, 208-222.
8. Apolloni B., de Falco D. and Taylor J.G. (1997), pRAM lay-out optimization. Neural Networks, 10, 1709-1716.
9. Apolloni B., Zamponi G. and Zanaboni A.M. (1998), Learning fuzzy decision trees, Neural Networks, to appear.
10. Bachevalier J. and Miskin M. (1986), The dynamics of attractor neural networks. New York: Cambridge University Press.
11. Bapi R.S., Bugmann G., Levine D.S. and Taylor J.G. (1998), Analysing the Executive Function of the Prefrontal System: Towards a Network Theory. Behaviour & Brain Sciences (submitted).
12. Becraft W.R., Lee P.L. and Newell R.B. ( 1991), Integration of neural networks and expert systems. In Proc. of the 12^th International Joint Conference on Artificial Intelligence, pages 832-837, Sydney, Australia. Morgan Kaufmann.
13. Berenji H.R. and Khedkar P. (1992), Learning and tuning fuzzy logic controllers through reinforcements. IEEE Trans. on Neural Networks, 3(5): 724-740.
14. Bezdec J.C., Tsao E.C.K. and Pal N. (1992), Fuzzy Kohonen clustering networks, Proc. IEEE Int. Conf. Fuzzy Syst. 1035-1046, San Diego.
15. Bezdec J.C. (1994), What is Computational Intelligent. In Computational Intelligence Imitating Life, Zurada, Marks and Robinson (eds), IEEE Press, New York.
16. Bishop C.M. (1995), Neural networks for pattern recognition, Oxford University Press, Oxford, United Kingdom.
17. Bose N.K. and Liang P. (1996), Neural Network Fundamentals with Graphs, Algorithms, and Applications, McGraw-Hill.
18. Breiman L., Friedman J.H., Olshen R. and Stone C.J. (1984), Classification and regression trees. Wadsworth Int., Belmont (CA), USA.
19. Burrascano P. (1991), Learning vector quantization for the probabilistic Neural Network. IEEE Trans. Neural Networks, 2(4): 458-461.
20. Carpenter G., Grossberg S. and Rosen D. (1991), Fuzzy ART: Fast stable learning and categorization of analog patterns by an adaptive resonance system. Neural Networks, Vol. 4, pp. 759-771.
21. Carpenter G., Grossberg S., Reynolds J. and Rosen D. (1992), Fuzzy ARTMAP: Suprvised real-time learning and classification of nonstationary data by a self-organizing neural network. Neural Networks, vol. 3, No 5, pp. 698-713.
22. Ciesielski V., Steven H. and Kelly B. (1992), Comparison of an expert system and a hybrid neural network/expert system for a respiratory problem. In R. Sun, L. Bookman, and S. Shekar, editors. AAAI-92 Workshop on Integrating Neural and Symbolic Processes: The Cognitive Dimension, July. Pages 141-143.
23. Cohen J.D., Forman S.D., Braver T.S., Casey B.J. et al. (1994), Activation of the prefrontal cortex in a non-spatial working memory task. Human Brain Mapping 1, 293-304.
24. Cohn D., Atlas L. and Ladner R. (1994), Improving Generalization with Active Learning, Machine learning, 15, 201-221.
25. Craven M. and Shavlik J. (1996), Extracting tree-structured representations of trained networks. In Touretzky, D., Mozer, M., & Hasselmo, M., editors, Advances in Neural Infromation Processing Systems (volume 8). MIT Press, Cambridge, M.A.
26. Daelemans W., van de Bosch A. and Weijters T. (1997), IGTree: using trees for compression and classification in lazy learning algorithms. Artificial Intelligence Review 11: 407-423.
27. Dean T., Allen J. and Aloimonos J. (1995), Artificial intelligence: theory and practice. Benjamin/Cummings Publishing Company, Redwood City (CA), USA.
28. Dias R., Roberts A.C. and Robbins T.W. (1996), Dissociation in prefrontal cortex of affective and attentional shifts. Nature 380, 690-72.
29. Dorfner G., Prem E. and Trost H. (1993), Words, symbols and symbol grounding. Austrian Research Institute for Artificial Intelligence, Vienna, TR 93-303.
30. Fisher D.H. (1987), Knowledge acquisition via incremental conceptual clustering. Machine Learning, 2, 139-172.
31. Fu L. (1994), Rule Generation from Neural Networks. IEEE Transaction on Systems, Man and Cybernetics, Vol. 24, No. 8, pp. 1114-1124.
32. Gallant S. (1988), Connectionist Expert Systems. Communications of the ACM, Vol. 31, No 2.
33. Giacometti A. (1992), Modeles hybrides de l’ expertise. Ph. D. thesis, ENST, Paris, November.
34. Giambasi N., Lbath R. and Touzet C. (1989), Une approche connexionniste pour calculer l’implication floue dans les systemes a base de connaissances. In Proc. of the 2^nd International Cionference on Neural Networks and their Applications, Nimes, France. EC2.
35. Goldberg D.E. (1989). Sizing Populations for Serial and Parallel Genetic Algorithms. Proceedings of the 3rd International Conference on Genetic Algorithms, 70-79.
36. Goodman R.M., Miller J.W. and Smyth P. (1989), An information theoretic approach to rule-based connectionist expert systems. In D. S. Touretzky, editor. Advances in Neural Information Processing, 1, pages 256-263. Morgan Kaufmann, San Mateo, CA.
37. Greenspan H.K., Goodman R. and Chellappa R. (1992), Combined neural network and rule based framework for probabilistic pattern recognition and discovery. In J. E. Moody, S. Hanson, and R. P. Lippman, editors. Advances in Neural Information Processing, 4, 444-451. Morgan-Kaufman, San Mateo, CA.
38. Guo H. and Gelfand S.B. (1992), Classification trees with neural network feature extraction. IEEE Trans. Neural Networks, 3(6): 923-933.
39. Gutknecht M. and Pfeifer R. (1990), An approach to integrating expert systems with connectionist networks. AICOM, 3(3):116-127.
40. Handelman D. A., Lane S.H. and Gelfand J.J. (1992), Robotic skill acquisition based on biological principles. In A. Kandel and G. Langholz, editors. Hybrid Architectures for Intelligent Systems, chapter 14, pages 301-327. CRC Press, Boca Raton, FL.
41. Harik G., Cant-Paz E., Goldberg D. E. and Miller B.L. (1996), The Gambler's Ruin Problem. Genetic Algorithms and the Sizing of Populations. IlliGAL Tech. Rpt. No. 96004.
42. Haugeland J. (1978), The nature of plausibility of cognitivism. Behaviour and Brain Science 2, pp. 215-260.
43. Hayashi Y., Czogala E. and Bukley J. J. (1992), Fuzzy Neural Controller. Proc. IEEE Int. Conf. Fuzzy Syst. 197-202, San Diego.
44. Hayes S., Ciesielski V.B. and Kelly W. (1992), A companion of an expert system and a neural network for respiratory system monitoring. Technical Report TR #92/1, Royal Melbourne Institute of Technology, March.
45. Haykin S. (1994), Neural Networks - A Comprehensive Foundation, MacMillan.
46. Hendler J. A. (1989), Problem solving and reasoning: A connectionist perspective. In R. Pfeifer, Z. Schreter, and F. Fogelman-Soulie, editors, Connectionism in Perspective, pages 229-243. Elsevier.
47. Hilario M. (1997), An overview of strategies for neurosymbolic integration. In Connectionist-Symbolic Processing: From Unified to Hybrid Approaches, R. Sun and F. Alexandre ed., Lawrence Erlbaum.
48. Hinton G. (ed.) (1991), Connectionist Symbol Processing, Special issue on Artificial Intelligence, Cambrigde, MA: MIT Press.
49. Hirota K. and Pedrycz W. (1996), Solving fuzzy relational equations through logical filtering, Fuzzy Sets and Systems 81, 355-363.
50. Horikawa S., Furuhashi T. and Uchikawa Y. (1992), On fuzzy modeling using fuzzy neural networks with the back-propagation algorithm. IEEE Trans. Neural Networks 3(5): 801-806.
51. Hornik K., Stichcombe M. and White H. (1989), Multilayer feedforward networks are universal approximators. Neural Networks 2: 359-366.
52. Hsu L.S., Teh H.H., Wang P.Z., Chan S.C. and Loe K.F. (1992), Fuzzy neural-logic systems. Proc. Int. Joint Conf. Neural Networks, Vol I, pp. 245-250, Baltimore.
53. Ishibuchi H., Fujioka R. and Tanaka H. (1993), Neural Networks that learn from fuzzy If-Then rules. IEEE Trans. Fuzzy Syst., 1(2):85-97.
54. Jabri M. et al. (1992), ANN based classification for heart defibrillators. In Advances in Neural Information Processing Systems, 4, 637-644, Morgan-Kaufmann.
55. Jordan M.I. and Jacobs R.A. (1994), Hierarchical mixtures of experts and the EM algorithm. Neural Computation 6: 181-214.
56. Jordan M.I., Ghahramani Z., Jaakkola T.S. and Saul L.K. (1998), An introduction to variational methods for graphical models. In: Jordan, MI (ed.), Learning in graphical models, Kluwer Academic Publishers.
57. Kappen H.J., Nijman M.J. and van Moorsel T. (1995), Learning active vision. In: Industrial Applications of Neural Networks. Eds. F. Fogelman-Soulie and P. Gallinari, World Scientific, pp. 193-201.
58. Kasabov N.K. (1996), Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering, Bradford, MIT Press.
59. Keller J. M. and Hunt D. J. (1985), Incorporating fuzzy membership functions into the perceptron algorithm. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-7(6): 693-699.
60. Keller J.M., Krishnapuram R. and Rhee F.C.H. (1992a), Evidence aggregation networks for fuzzy logic interface. IEEE Trans. Neural Networks 3(5): 751-769.
61. Keller J.M., Yager R. R. and Tahani H. (1992b), Neural Network implementation of fuzzy logic. Fuzzy Sets and Syst. 45: 1-12.
62. Klir J. and Bo Yuan (1995), Fuzzy Sets and Fuzzy Logic: Theory and Applications, Prentice Hall.
63. Koza J. (1992), Genetic Programming : On the Programming of Computers by Means of Natural Selection (Complex Adaptive Systems), MIT press, 1992
64. Koza J. (1994), Genetic programming II, The MIT press, 1994
65. Krovvidy S. and Wee W.G. (1992), An intelligent hybrid system for wastewater treatments. In A. Kandeland G. Langholz, editors. Hybrid Architectures for Intelligent Systems, chapter 17, pages 358-377, CRC Press, Boca Raton, FL.
66. Kuo Y.H., Kao C. I. and Chen J. J. (1993), A Fuzzy Neural Network model and its hardware implementation. IEEE Trans. Fuzzy Syst., 1(3): 171-183.
67. Kwasny S. C. and Faisal K. A. (1992), Symbolic parsing via subsymbolic rules. In J. Dinsmore, editor, The Symbolic and Connectionist Paradigms: Closing the Gap, pages 209-235. Lawrence Erlbaum Associates Inc., Northvale, NJ.
68. Langdon W. (1998), Genetic Programming + Data Structures = Automatic Programming. Kluwer International Series in Engineering and Computer Science, ISBN 0-7923-8135-1
69. Lin C.T. and Lee C.S. (1995), Neural fuzzy systems-A Neuro-Fuzzy Synergism to Intelligent Systems, Prentice-Hall, New York.
70. Lin C.T. and Lu Y.C. (1995), A neural fuzzy system with linguistic teaching signals. IEEE Trans. Fuzzy Syst., 3(2): 169-189.
71. Lin C.T. and Lu Y.C. (1996), A neural fuzzy system with fuzzy supervised learning. IEEE Trans. Syst. Man Cyber., (26)10.
72. Looney C.G. (1997), Pattern Recognition Using Neural Networks. Oxford University Press.
73. Medsker L.R. (1994), Hybrid Neural Network and Expert Systems. Kluwer Academic Publishers, Boston.
74. Medsker L.R. (1995), Hybrid Intelligent Systems, Kluwer Academic Publishers.
75. Mitra S. and Pal S. (1995), Fuzzy multi-layer Perceptron, Inferencing and Rule Generarion. IEEE Trans. on Neural Networks, 6(1), pp. 51-63.
76. Mitra S. and Pal S. (1997), Knowledge-Based Fuzzy MLP for Classification and Rule Generation. IEEE Trans. on Neural Networks, 8(6), pp. 1338-1350.
77. Murthy K.V.S. (1995), On growing better decision trees from data. PhD-thesis, John Hopkins University, Baltimore (MD), USA.
78. Narazaki H., Watanabe T. and Yamamoto M. (1996), Reorganizing Knowledge in Neural Networks in Data Classification Problems. IEEE Transactions on Systems Man and Cybernetics-Part B: Cybernetics, vol 26, No. 1, February 1996.
79. Omlin C.W. and Lee Giles C. (1996), Constructing Deterministic Finite-State Automata in Recurrent Neural Networks. Journal of ACM, Vol 43, No. 6, pp937-972
80. Omlin C.W. and Lee Giles C. (1996), Extraction of Rules from Discrete-time Recurrent Neural Netwroks. Neural Networks, Vol. 9, No. 1, pp. 41-52.
81. Ourston D. and Mooney R.J. (1994), Theory refinement combining analytical and empirical methods. Artificial Intelligence 66, 273-310.
82. Pal S. and Mitra S. (1992), Multi-Layer Perceptron, Fuzzy Sets and Classification. IEEE Trans. on Neural Networks, 3(5), pp. 683-697.
83. Pao Y.H. (1989), Adaptive Pattern Recognition and Neural networks, Reading, Addison-Wesley.
84. Pedrycz W. (1991), Neurocomputations in relational systems. IEEE Trans. on Pattern Anal. Mach. Intell. PAMI-13 (3), 289-297.
85. Pedrycz W. and Rocha A.F. (1993), Fuzzy-set based model of neurons and knowledge-based networks. IEEE Transactions on Fuzzy Systems 1, 254-266.
86. Piramuthu S. and Shaw M. I. (1994), On using decision trees as feature selector for feedforward neural networks. In L. M. Fu, editors. International Symposium on Integrating Knowladge and Neural Heuristics, pages 67-74, Pensacola, FL, May.
87. Pollack J.B. (1990), Recursive distributed representation, Art. Intell., 46: 77-105.
88. Pomerleau D.A., Gowdy J. and Thorpe C.E. (1991), Combining artificial neural networks and symbolic processing for autonomous robot guidance. Engineering Applications of Artificial Intelligence, 4(4):279-285.
89. Quinlan J. R. (1986), Induction of decision trees. Machine Learning 1, 81-106.
90. Quinlan J.R. (1993), C4.5: programs for machine learning. Morgan Kaufmann Publishers, San Mateo (CA), USA.
91. Ripley B.D. (1996), Pattern Recognition and Neural Nerworks, Cambridge University Press.
92. Sankar A. and Mammone R. J. (1991), Neural tree networks. In R. J. Mammone and Y. Y. Zeevi, eds., Neural Networks, 3(6): 465-467.
93. Schalkoff R.J. (1997), Artificial Neural Networks, McGraw-Hill.
94. Searle J.R. (1990), The intentionality of intention and action. Cognitive Science 4, 47-70.
95. Setiono R. and Liu H. (1995), Understanding Neural Networks via Rule Extraction. Procceedings of the 14^th International Joint Conference on Artificial Intelligence, 480-485.
96. Sima J. (1992), The Multi-Layered Neural Network as an Adaptive Expert System with the Ability to Work with incomplete Information and to Provide Justification of Inference. Neural Network World, 2:47-58.
97. Sima J. (1995), Neural Expert Systems. Neural Networks Vol. 8, No.2 pp 261-271, 1995.
98. Simpson P.K. (1992), Fuzzy min-max neural networks-Part 1: Classification. IEEE Trans. on Neural Networks, 3 (5): 776-786.
99. Simpson P.K. (1993), Fuzzy min-max neural networks-Part 2: Clustering. IEEE Trans. on Fuzzy Systems, 1 (1): 32-45.
100. Smolensky P. (1986), Information processing in dynamical systems: foundations of harmony theory. In Rumelhart D.E., Parallel Distributed Processing, Vol 1, 194-218, Cambridge, MA:MIT Press.
101. Specht D.F. (1990), Probabilistic Neural Networks. Neural Networks, 3(1): 281-302.
102. Sperduti A., Starita A. and Goller C. (1995), Learning distributed representations for the classification of terms. In Proceedings of the International Joint Conference of Artificial Intelligence, 1995, pp 509-515.
103. Sperduti A. and Starita A. (1997), Supervised Neural Networks for the Classification of Structures. IEEE Transactions on Neural Networks, Vol. 8, No.3, May 1997.
104. Sugeno M. and Kang G.T. (1988), Structure identification of fuzzy model. Fuzzy Sets and Syst. 28(1): 15-33.
105. Sun R. (1994), Integrating rules and connectionism for robust commonsense reasoning, Wiley N.Y.
106. Sun R. and Bookman L. (eds) (1994), Computational Architectures Integrating Neural and Symbolic Processes, Kluwer Academic Publishers.
107. Sun R. and Alexandre F. (eds) (1997), Connectionist-Symbolic Integration: From Unified to Hybrid Approaches, Lawrence Erlbaum.
108. Suttner Ch. and Ertel W. (1990), Automatic acquisition of search guiding heuristics. In 10^th Int. Conf. On Automated Deduction, pages 470-484. Springer-Verlag, LNAI 449.
109. Takagi H. and Hayashi I. (1991), NN-driven fuzzy reasoning. Int. J. Approximate Reasoning 5(3): 191-212.
110. Taylor J. G. (1997), Neural Networks for consciousness. In Taylor, J.G. and Freeman, W. Neural Networks for consciousness. 1207-1226, Special Issue, Neural networks, Pergamon, Elsevier Science Ltd.
111. Taylor J.G. and Meller-Gaertner H.-W. (1997), Non Invasive Analysis of Awareness. 1188-1194, Special Issue, Neural networks, Pergamon, Elsevier Science Ltd.
112. Thomson K., Langley P. and Iba W. (1991), Using background knowledge in concept formation. In Proc. Eighth International Machine Learning Workshop, Evanston, IL.
113. Thrun S. (1995), Extracting Rules from Artificial Neural Networks with Distributed representations. In Advances in Neural Information Systems 7.
114. Towell G.G., Shavlic J.W. and Noordewier M.O. (1990), Refinement of approximately correct domain theories by knowledge-based neural networks. Proceedings of the Eighth National Conference on Artificial Intelligence, San Jose, CA, AAAI Press, pp. 177 - 182.
115. Uehara K. and Fujise M. (1993), Multistage Fuzzy Inference Formulated as Linguistic-Truth-Value Propagation and Its Learning Algorithm Based on Back-Propagating Error Information. IEEE Transactions on Fuzzy Systems, 1(3).
116. Vaario J. and Ohsuga S. (1992), An emergent construction of adaptive neural architectures. Heuristics-The Journal of Knowledge engineering, 5(2), 1-12.
117. Vanni S., Revonsuo A., Saarinen J. and Hari R. (1996), Visual awareness of objects correlates with activity of right occipital cortex. NeuroReport, 8, 183-186.
118. Verschure P.F.M.J. (1992), Taking connectionism seriously: the vague promise of subsymbolism and an alternative. Proc. 14th annual conference of the Cognitive Science Society, Hillside, N.J.: Erlbaum, 653-658.
119. Verschure P.F.M.J. (1993), Formal minds and biological brains: AI and Edelman's extended theory of neuron group selection. IEEE Expert: Intelligent Systems and their Applications 8(5), 66-75.
120. Verschure P.F.M.J. (1997), Connectionist explanation: taking position in the mind-brain dilemma. In Neural Networks and a New Artificial Intelligence (G. Dorffner ed.) 133-188, International Thomson Computer Press, London.
121. Wang L.X. (1993), Solving fuzzy relational equations through network training. Proc. IEEE Int. Conf. Fuzzy Syst., Vol. II, 956-960, San Francisco.
122. Weigend A.S., Zimmermann H.G. and Meuneier R. (1996), Clearning. In Refenes, P., Abu-Mostafa, Y., Moody, J., and Weigend, A. S., editors, Neural Networks in Financial Engineering. World, Scientific, Singapore.
123. Welsh M.C. and Pennington B.F. (1988), Assesing frontal lobe function in children: Views from develpmental psychology. Developmental Neuropsycology, 4, 199-200.
124. Westerdijk M. and Gielen C.C.A.M. (1998). In preparation.
125. Yager R.R. (1992a), Expert systems using fuzzy logic. In R.R. Yager and L. A. Zadeh eds., An introduction to fuzzy logic applications in intelligent systems, Kluwer Academic Publishers.
126. Yager R.R. (1992b), OWA neurons: a new class of fuzzy neurons. Proc. Int. Joint Conf. Neural Networks, Vol I, pp. 226-231, Baltimore.